Parcours 1 : Comment évaluer une grandeur ?

3. Comment évaluer la longueur de l'arc de parabole d'équation $y=x^2$ entre 0 et 1 ?

Avec une subdivision :

alt text

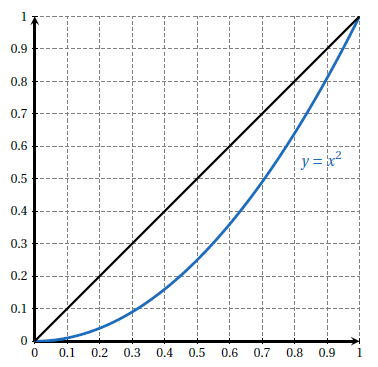
Le segment noir mesure $L_1 = \sqrt{2}$ (diagonale d'un carré de côté 1)

Avec 2 subdivisions :

alt text

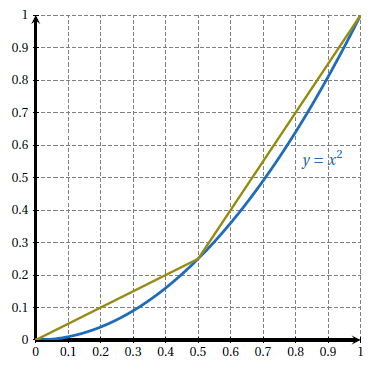
On se sert :

  • des coordonnées des points de la courbe qui sont de la forme $(x ; x^2)$;
  • de la formule de calcul de longueurs dans un r.o.n. (repère orthonormé) : $$AB = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}$$

Longueur verte : $L_2 = \sqrt{0,5^2 + 0,25^2} + \sqrt{0,5^2 + 0,75^2} \approx 1,4604$

(On trouve de tête les écarts entre les abscisses et entre les ordonnées)

Avec 4 subdivisions :

alt text

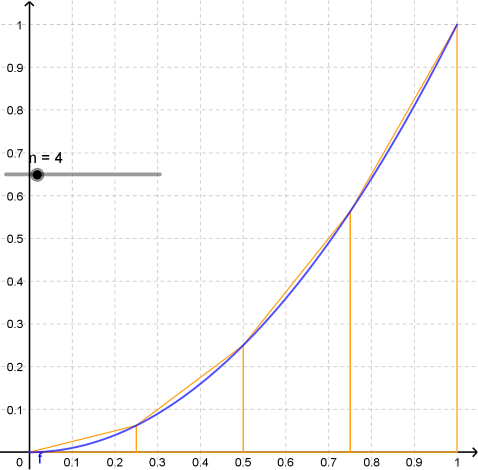
Notons $s_0 , s_1 , s_2$ et $s_3$ les quatre segments dont on souhaite calculer la longueur afin d'approcher la longueur de l'arc bleu.

Les abscises des extrémités des segments sont : $0 ; \frac{1}{4} ; \frac{1}{2} ; \frac{3}{4}$ et $1$ ou encore $\left(\frac{0}{4} , \frac{1}{4} , \frac{2}{4} , \frac{3}{4}, \frac{4}{4}\right)$. On parle de subdivision de l'intervalle $[0;1]$.

Introduisons la fonction : $f(x)=x^2$ associée à la parabole par souci de notation.

Les longueurs des quatre segments sont donc :

  • $s_0=\sqrt{\left( \dfrac{1}{4}-0\right)^2+ \left( f(\dfrac{1}{4})-f(0)\right)^2} =\sqrt{\left( \dfrac{1}{4}\right)^2+ \left( f(\dfrac{1}{4})-f(\dfrac{0}{4})\right)^2} \approx 0,25769$

  • $s_1=\sqrt{\left( \dfrac{2}{4}-\dfrac{1}{4}\right)^2+\left( f(\dfrac{2}{4})-f(\dfrac{1}{4})\right)^2} = \sqrt{\left( \dfrac{1}{4}\right)^2+\left( f(\dfrac{2}{4})-f(\dfrac{1}{4})\right)^2} \approx 0,3125$

  • $s_2=\sqrt{\left( \dfrac{3}{4}-\dfrac{2}{4}\right)^2+\left(f(\dfrac{3}{4})-f(\dfrac{2}{4})\right)^2} = \sqrt{\left( \dfrac{1}{4}\right)^2+\left(f(\dfrac{3}{4})-f(\dfrac{2}{4})\right)^2} \approx 0,40020$

  • $s_3=\sqrt{\left( \dfrac{4}{4}-\dfrac{3}{4}\right)^2+\left(f(\dfrac{4}{4})-f(\dfrac{3}{4})\right)^2} = \sqrt{\left( \dfrac{1}{4}\right)^2+\left(f(\dfrac{4}{4})-f(\dfrac{3}{4})\right)^2} \approx 0,50389$

Ce qu'il faut remarquer :

  • L'écart des abscisses est toujours égal à $\dfrac{1}{4}$ (On a coupé en 4 ...)

  • Pour les écarts des ordonnées, on décale d'un cran les antécédents en jeu d'un segment au suivant : $\left( f(\dfrac{\color{red}{1}}{4})-f(\dfrac{\color{blue}{0}}{4})\right)$ puis $\left( f(\dfrac{\color{red}{2}}{4})-f(\dfrac{\color{blue}{1}}{4})\right)$ ...

Longueur orange : $\displaystyle L_4 = s_0 + s_1 + s_2 + s_3 \approx 1,47428$

Notation :

Afin de faciliter les notation, on note : $\displaystyle L_4 = s_0 + s_1 + s_2 + s_3 = \sum_{k=0}^3 \sqrt{\left( \dfrac{1}{4}\right)^2+\left(f(\dfrac{k+1}{4})-f(\dfrac{k}{4})\right)^2}$

$\displaystyle \sum_{k=0}^3 \quad$ se lit : "La somme de k allant de 0 à 3 de ..."

Avec 10 subdivisions :

alt text

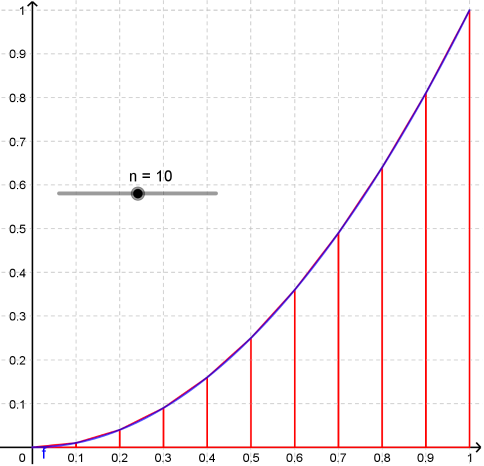
Notons $s_0 , s_1 , s_2, s_{9}$ les 10 segments dont on souhaite calculer la longueur afin d'approcher la longueur de l'arc bleu.

Sur l'axe des abscisses, on a une subdivision de l'intervalle $[0;1]$ : $\left(0, \frac{1}{10} , \frac{2}{10} , \frac{3}{10}, \ldots \frac{10}{10}\right)$.

Les longueurs des 10 segments sont donc :

  • $s_0=\sqrt{\left( \dfrac{1}{10}-0\right)^2+ \left( f(\dfrac{1}{10})-f(0)\right)^2} =\sqrt{\left( \dfrac{1}{10}\right)^2+ \left( f(\dfrac{1}{10})-f(\dfrac{0}{10})\right)^2} \approx 0,10050$

  • $s_1=\sqrt{\left( \dfrac{2}{10}-\dfrac{1}{10}\right)^2+\left( f(\dfrac{2}{10})-f(\dfrac{1}{10})\right)^2} = \sqrt{\left( \dfrac{1}{10}\right)^2+\left( f(\dfrac{2}{10})-f(\dfrac{1}{10})\right)^2} \approx 0,10440$

  • ...

  • $s_9=\sqrt{\left( \dfrac{10}{10}-\dfrac{9}{10}\right)^2+\left(f(\dfrac{10}{10})-f(\dfrac{9}{10})\right)^2} = \sqrt{\left( \dfrac{1}{10}\right)^2+\left(f(\dfrac{10}{10})-f(\dfrac{9}{10})\right)^2} \approx 0,21471$

Ce qu'il faut remarquer :

  • L'écart des abscisses est toujours égal à $\dfrac{1}{10}$ (On a coupé en 10 ...)

  • Pour les écarts des ordonnées, on décale d'un cran les antécédents en jeu d'un segment au suivant : $\left( f(\dfrac{\color{red}{1}}{10})-f(\dfrac{\color{blue}{0}}{10})\right)$ puis $\left( f(\dfrac{\color{red}{2}}{10})-f(\dfrac{\color{blue}{1}}{10})\right)$ ...

Finalement, la longueur orange : $\displaystyle L_{10} = s_0 + s_1 + \ldots + s_9 = \sum_{k=0}^{9} \sqrt{\left( \dfrac{1}{10}\right)^2+\left(f(\dfrac{k+1}{10})-f(\dfrac{k}{10})\right)^2} \approx 1,47820$

Remarque :

On aurait pu aussi écrire : $\displaystyle L_{10} = s_0 + s_1 + \ldots + s_9 = \sum_{k=1}^{10} \sqrt{\left( \dfrac{1}{10}\right)^2+\left(f(\dfrac{k}{10})-f(\dfrac{k-1}{10})\right)^2}$

4. Avec Python :

Avec 100 subdivisions, personnes n'a envie de faire les calculs. Un algorithme peut nous aider...

Voici le programme Python donné sur le sujet :

In [1]:
from math import sqrt

def f(x):
    return x**2

n = 10
longueur = 0

for k in range(n):
    segment = sqrt((1/n)**2 + (f((k+1)/n) - f(k/n))**2)
    print(segment)
    longueur = longueur + segment
    
print("La longueur de l'arc est", longueur)

0.1004987562112089
0.1044030650891055
0.11180339887498948
0.12206555615733705
0.1345362404707371
0.14866068747318506
0.16401219466856723
0.18027756377319962
0.19723082923316013
0.21470910553583883
La longueur de l'arc est 1.4781973974873288

Vous pouvez exécuter ce code en utilisant le bouton "Play" dans la barre du haut, essayez !

Exercice

  1. Lire cet algorithme et essayer de comprendre le lien avec tout ce que l'on vient de faire

  2. Comment traduire la ligne : for k in range(0, n):, cela vous rappelle-t-il quelque chose ?

  3. Vérifier les valeurs trouvées pour $n = 4$ puis $n = 10$

  4. Quelle valeur approchée de l'arc trouve-t-on pour $n = 100$ ? $n = 1000$ ?

  5. Ajouter une ligne dans le programme pour vérifier les longueurs des 10 segments que vous avez calculé chez vous (ou pas)

5. Avec un autre arc de parabole ?

alt text

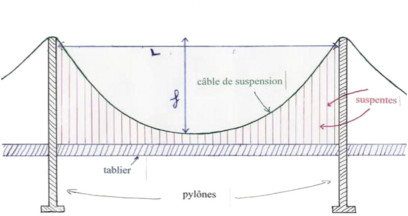
Pour le Golden Gate Bridge , on donne : L = 1280m et f = 151,5m.

Exercice

Déterminer dans ce cas une équation de la courbe à étudier.

alt text

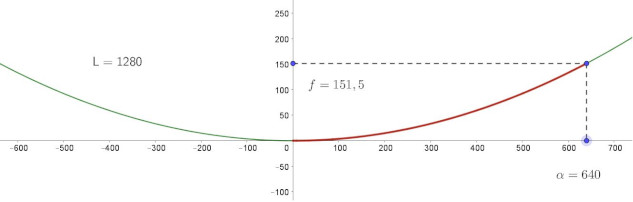
Réponse :

On a une fonction du second dégré dont on connaît le sommet (0 ; 0) :

Forme canonique : $f(x) = a(x-\alpha)^2 + \beta = a(x-0)^2 + 0 = ax^2$

Il reste à déterminer le coefficient dominant $a$ à l'aide de l'information : $f(640) = 151,5$

$a\times 640^2 = 151,5$, autrement dit, $a = \dfrac{151,5}{640^2}$

remarque : On aurait pu aussi utiliser le fait que $0$ soit racine double : $f(x)=a(x-x_0)^2$

6. Modifier l'algorithme

Modifier l’algorithme afin qu’il permette de donner une valeur approchée de la longueur du câble entre les deux pylônes du Golden Gate.

Attention ! Il n'ya pas que la fonction à changer... Commencez à la main avec 4 subdivisions, vous verrez les changements à effectuer...

En effet, il vaut mieux commencer à la main pour se rendre compte des changements...

Avec 4 subdivisions :

alt text

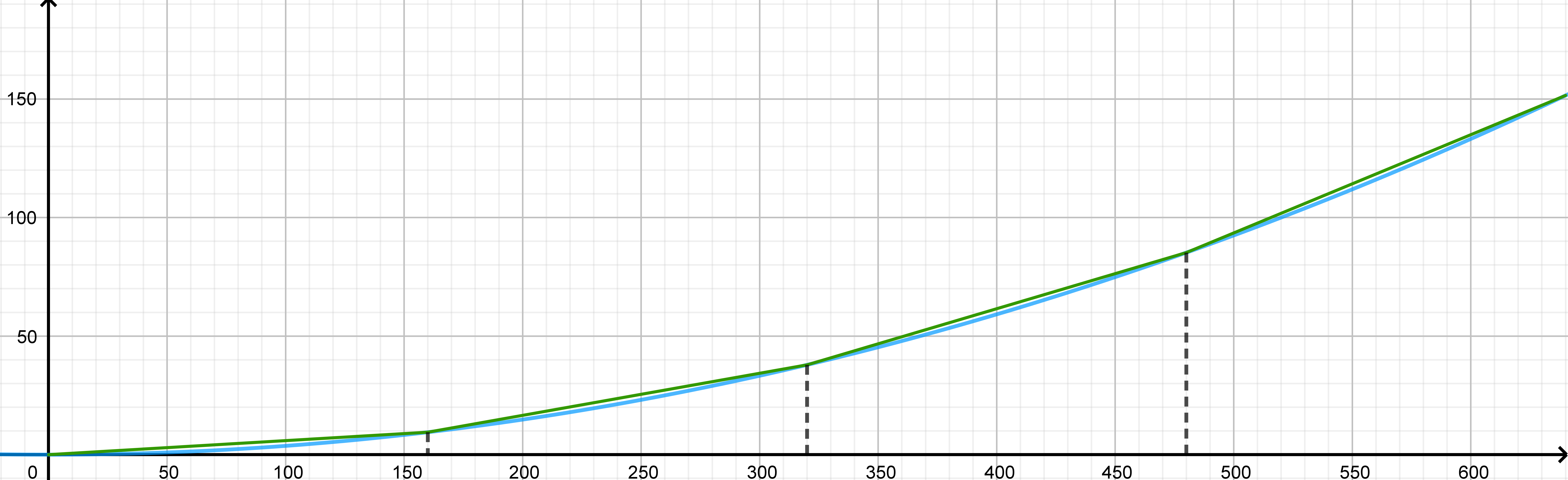
Cette fois-ci, on change l'intervalle à découper, ce n'est plus $[0;1]$ mais $[0;640]$ !

La subdivision sera donc : $\left( 0 ; \dfrac{640}{4} ; \dfrac{2\times 640}{4} ; \dfrac{3\times 640}{4} ;640 \right)$

Notons $s_0 , s_1 , s_2$ et $s_3$ les quatre segments dont on souhaite calculer la longueur afin d'approcher la longueur de l'arc bleu.

La fonction : $f(x)=\dfrac{151,5x^2}{640}$ associée à l'arc de parabole.

Les longueurs des quatre segments sont donc :

  • $s_0=\sqrt{\left( \dfrac{640}{4}-0\right)^2+ \left( f(\dfrac{640}{4})-f(0)\right)^2} =\sqrt{\left( \dfrac{640}{4}\right)^2+ \left( f(\dfrac{1\times 640}{4})-f(\dfrac{0\times 640}{4})\right)^2} \approx 160,2799$

  • $s_1=\sqrt{\left( \dfrac{2\times 640}{4}-\dfrac{1\times 640}{4}\right)^2+\left( f(\dfrac{2\times 640}{4})-f(\dfrac{1\times 640}{4})\right)^2} = \sqrt{\left(\dfrac{640}{4}\right)^2+\left( f(\dfrac{2\times 640}{4})-f(\dfrac{1\times 640}{4})\right)^2} \approx 162,5020 $

  • $s_2=\sqrt{\left( \dfrac{3\times 640}{4}-\dfrac{2\times 640}{4}\right)^2+\left(f(\dfrac{3\times 640}{4})-f(\dfrac{2\times 640}{4})\right)^2} = \sqrt{\left( \dfrac{640}{4}\right)^2+\left(f(\dfrac{3\times 640}{4})-f(\dfrac{2\times 640}{4})\right)^2} \approx 166,8575$

  • $s_3=\sqrt{\left( \dfrac{4\times 640}{4}-\dfrac{3\times 640}{4}\right)^2+\left(f(\dfrac{4\times 640}{4})-f(\dfrac{3\times 640}{4})\right)^2} = \sqrt{\left( \dfrac{640}{4}\right)^2+\left(f(\dfrac{4\times 640}{4})-f(\dfrac{3\times 640}{4})\right)^2} \approx 173,1854$

Formule générale pour $n$ subdivisions :

Avec $n$ subdivisions de l'intervalle $[0;640]$ à pas constant on obtient sur l'axe des abscisses : $\left( 0 ; \dfrac{640}{n} ; \dfrac{2\times 640}{n} ; \ldots ; \dfrac{(n-1)\times 640}{n} ;640 \right)$

Pour la longueur des segments on obtient donc :

  • $s_0=\sqrt{\left( \dfrac{640}{n}\right)^2+ \left( f(\dfrac{1\times 640}{n})-f(\dfrac{0\times 640}{n})\right)^2}$

  • $s_1= \sqrt{\left(\dfrac{640}{n}\right)^2+\left( f(\dfrac{2\times 640}{n})-f(\dfrac{1\times 640}{n})\right)^2} $

  • ...

  • $s_k = \sqrt{\left( \dfrac{640}{n}\right)^2+\left(f(\dfrac{(k+1)\times 640}{n})-f(\dfrac{k\times 640}{n})\right)^2}$

  • ...

  • $s_{n-1} = \sqrt{\left( \dfrac{640}{n}\right)^2+\left(f(640)-f(\dfrac{(n-1)\times 640}{n})\right)^2} $

D'où l'algorithme suivant :

In [6]:
from math import sqrt

def f(x):
    return (151.5*x**2)/(640**2)

n = 100
longueur = 0

for k in range(0, n):
    segment = sqrt((640/n)**2 + (f((k+1)*640/n) - f(k*640/n))**2)
    longueur = longueur + segment
    
print("La longueur de l'arc est", longueur)

La longueur de l'arc est 663.1623376893717

Pour répondre au problème, il ne faudra pas oublier de multiplier par 2 car notre étude n'approche que la moitié du câble entre les deux pylônes.